Perl en Japanse puzzels

Japanse puzzels (Japanese puzzles?), hoe los ik die op? Of, om precieser te zijn: hoe los ik die op met de programmeertaal Perl?

Eerst: wat zijn Japanse puzzels ook al weer? Hiernaast (figuur 1) een plaatje. De getallen die erbij staan (boven en links) geven aan hoeveel series gekleurde blokjes (gescheiden door minstens een wit blokje) er in die rij of kolom staan. Bijvoorbeeld '2,3' betekent: nul of meer wit, dan twee gekleurd, een of meer wit, drie gekleurd, en dan mogelijk nog wat wit.

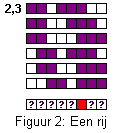Het probleem zit het in het feit dat je niet weet hoeveel witte vakjes waar zitten (afhankelijk van de grootte van de puzzel). Als voorbeeld de '2,3' bij de 4e rij van voorbeeld in figuur 1: bij een veld van 6 breed zou het maar op een manier passen. Op het veld van 8 breed heb je al 8 mogelijkheden (zie figuur 2 hiernaast). Naarmate de grootte toeneemt neemt het aantal mogelijkheden ook fors toe (10 -> 15, 11->21, 12 -> 28, ....).

De manier om uit te vissen welke correct is is om alle mogelijkheden per rij (of kolom) eens goed te bekijken. De '2,3' in een veld van 8 kan dan op acht manieren, toch is er al iets uit af te leiden. Zoals je in figuur 2 kan zien, is het zesde vakje in ieder geval gekleurd (want dit is in alle mogelijkheden het geval), al weten we de rest nog niet.Deze informatie kan je weer gebruiken om kolommen vast te leggen: is bijvoorbeeld in die kolom maar een vakje gekleurd, dan moet het dat vakje zijn (en is de rest gegarandeerd leeg; ook belangrijke informatie). En zo voort.

Dit is ook hoe mijn programma werkt. Eerst leest het de beschrijving van de puzzle in, bijvoorbeeld zoals de tekstfile in het rechter plaatje (figuur 3: de file met de puzzel uit figuur 1). Dan gaat het voor iedere rij (en kolom) alle mogelijke patronen genereren (zonder nog rekening te houden met wat er in andere rijen staat), zoals in de voorbeeldrij in figuur 2. Dit levert uiteraard nog een waanzinnige hoeveelheid mogelijkheden op, maar nu gaan we kijken welke informatie we uit de gemaakte patronen kunnen halen, zitten er bijvoorbeeld al vlakjes in die gegarandeerd gekleurd zijn.

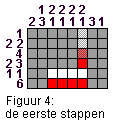
In het voorbeeld in figuur 3 is dit bijvoorbeeld het geval voor de onderste rij: er zijn hier 6 van de acht vakjes gekleurd: dus in ieder geval de middelste 4. Probeer maar, een rijtje van 6 past er maar op drie manieren in, met de middelste 4 gemeenschappelijk. Samen met het '2,3' verhaal van hierboven komen we dan tot de rode vakjes in figuur 4. Maar (gezien de cijfertjes: de kolommen eindigen op een '1') betekend dat ook dat direkt boven de vakjes op de onderste rij witte vlakjes zitten! En daarmee weten we dan weer ....... en zo voort.

Zo werkt het programma in feite ook. Eerst wordt van alle gemaakte mogelijkheden per rij en kolom bekeken wat we daardoor weten. Dan gaan we hiermee net zolang kijken welke kolommen er passen bij de informatie van de rijen, en omgedraaid, tot we nog maar een passende manier overhouden. Dat wordt vervolgens afgedrukt. Klinkt simpel. Was het ook wel, ik had het programma in een of twee uurtjes in elkaar gezet. Maar toch komt er wel wat bij kijken, zoals het bijhouden van alle mogelijkheden per rij: wat is daarvoor de beste mogelijkheid (een lijst van patronen)? Al met al is het niet echt een programma voor beginners geworden.

Het programma levert de volgende output, waarbij eerst een aantal tussenstappen worden weergegeven, met per rij/kolom het aantal mogelijke posities van de blokjes op dat moment (wat je per rij/kolom dus tot 1 mogelijkheid ziet verminderen):

> perl Japans.pl Japan1.txt
Japanese puzzle #1
x alternatives: 5, 3, 6, 6, 6, 6, 4, 6, x total = 466560
y alternatives: 8, 10, 5, 6, 21, 3, x*y total = 70543872000
x alternatives: 5, 3, 3, 3, 3, 1, 4, 6, x total = 9720
y alternatives: 7, 5, 3, 5, 2, 3, x*y total = 30618000
x alternatives: 1, 2, 3, 3, 2, 1, 4, 6, x total = 864
y alternatives: 1, 2, 3, 2, 2, 1, x*y total = 20736
x alternatives: 1, 1, 1, 1, 2, 1, 1, 4, x total = 8
y alternatives: 1, 1, 1, 2, 1, 1, x*y total = 16
x alternatives: 1, 1, 1, 1, 1, 1, 1, 1, x total = 1
y alternatives: 1, 1, 1, 1, 1, 1, x*y total = 1
Final solution:

X.......
XX.XX...
..XXXX..
.XX..XXX
.X....X.
.XXXXXX.

We zien de verschillende stappen van eliminatie, en het minder worden van de mogelijkheden. Per stap zien we eerst per kolom de aantallen mogelijkheden (x alternatives) en dan hetzelfde per rij (als je ziet, bij de eerste 'y alternatives' geeft de laatste rij inderdaad '3', de drie manieren waarop 6 in 8 past). Het grote aantal mogelijkheden zakt (gelukkig) rap in elkaar, en komt vrij snel tot een oplossing, zoals met 'X'jes en puntjes afgedrukt.

Het Perl programma (als zip file): klik >> hier << om te downloaden (voor de voorbeeldfile japan1.txt: hier). Start met de '-?' optie om een korte uitleg over het gebruik te krijgen, of kijk in bovenstaand voorbeeld hoe ik het programma aanriep. Met dank aan degene die het voorbeeldpuzzeltje heeft gemaakt, weet alleen niet wie het is (had het nog ergens liggen). Update versie 1.2, december 2003: betere checks op foutieve invoer (typefouten en zo).

De grootste puzzel zo ver die ik hiermee gemaakt heb is 25 bij 25 vakjes, het programma doet er zo'n 4 seconden over en gaat in 8 stappen al naar de uiteindelijke oplossing. Maximale puzzel is 32 bij 32, omdat ik 32-bit 'integers' gebruik om bitpatronen op te slaan (opmerking voor gevorderden ;-).

Wil je zien hoe de stappen zijn die het programma neemt, gebruik dan de -d1 optie (en vang de output op in een tekstfile). Hier krijg je een file met tussenresultaten te zien:

perl Japans.pl -d1 Japan1.txt >resultaat.txt

Interesse in web sites over puzzels in het algemeen? Kijk eens op de Puzzel-startpagina.