Sudoku's in Perl

Het idee

Nu is programmeren voor een groot deel nadenken. Wat is het probleem (da's hier duidelijk), hoe kan je het oplossen (je strategie -> algoritme), en hoe sla je de gegevens op? Het laatste is vaak een van de sleutels tot een goed programma.

Wat is het kernprobleem met Sudoku's: je hebt een bord met vakjes. Vakjes kunnen op verschillende manieren bij groepen ingedeeld worden (rijen, kolommen, en zo), en kunnen dus in meerdere groepen voorkomen. In elke groep mag vervolgens elk cijfer (of symbool) maar een keer voorkomen. Bij standaard-Sudoku's zijn die groepen bijvoorbeeld de rijen, kolommen, en de 3x3 vlakjes zoals normaal in de puzzel aangegeven. Soms zijn er ook extra regels, zoals de groepen gevormd door de diagonalen (de diagonaal-Sudoku), of worden er in plaats van 3x3 vakjes willekeuriger vormen gebruikt (vorm-Sudoku). We hebben dus:

1. Een 'bord' (meestal 9x9), met vakjes (cellen)
2. Symbolen (meestal de cijfers 1 t/m 9) die hierop ingevuld moeten worden
3. Regels die zeggen hoe met de cellen (vakjes) de groepen gevormd worden, waarin elk symbool maar een keer mag voorkomen.

De dataopslag (data structures)

Hoe sla ik dit op? Het bord deel ik op in vakjes, die ik bij een 9x9 bord nummer van 0 tot 80 (programmeurs doen het vanaf 0). Dit wordt in het programma voorgesteld door een normaal array (genaamd @cells). In ieder vakje kunnen symbolen voorkomen, en als de puzzel nog niet klaar is, zijn er nog meerdere mogelijkheden per vakje. Als ik ieder symbool nu eens een bit geef (in Perl zijn integers normaal 32 bits, kunnen dus 32 verschillende symbolen in worden bijgehouden). Ik gebruik bit 0..8 voor de waardes 1..9. Is een bit gezet ('1'), dan is dat symbool nog mogelijk, is het gereset ('0') dan kan dat symbool daar niet meer.

Voor de regels gebruik ik lijsten (implementatie als array) waarin ik bijhoud welke cellen in de groep van die regel zitten. Bijvoorbeeld de eerste rij is dan (0,1,2,3,4,5,6,7,8), de eerste kolom (0,9,18,27,36,45,54,63,72). Al deze regels verzamel ik in een array (genaamd @rules), zodat ik makkelijk door deze heen kan stappen.

De 9 rijen kan ik in Perl in een keer als 9 lijsten in array @rules aanmaken, als volgt (ga hier maar eens goed voor zitten, dit is Perl voor gevorderden ;-)

for my $j (0..8) { push @rules, [ map { $j*9 + $_ } (0..8) ] };

Op soortgelijke manier kan ik ook de kolommen, en met wat meer gepruts de 3x3 gebieden, maken.

Daarnaast nog wat administratie, zoals een variabele $found die we ophogen iedere keer dat we een symbool kennen; als deze op 81 staat (9x9 bekende symbolen) dan is de puzzel opgelost.

Strategie 1

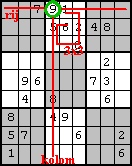Mijn eerste strategie is simpel (en effectief). In de opgave zijn een aantal cellen gegeven. Deze waardes kunnen dus niet in de andere cellen van iedere groep voorkomen (in iedere groep mag elk symbool maar een keer voorkomen). Voor iedere groep waar deze cel in zit kan dus deze mogelijke waarde uit de andere cellen weggestreept worden (zie voorbeeld: als de '9' in cel 3 zit, ik tel vanaf 0, dan kan de 9 als mogelijkheid uit die kolom, die rij en dat 3x3 vak weggestreept worden: op de rode lijnen kan geen 9 staan).

Met een beetje mazzel (bij eenvoudige Sudoku's) levert dit weer nieuwe cellen op waar nog maar een mogelijkheid over is. Door dan weer dezelfde strategie toe te passen is er nog meer weg te strepen. En zo door, tot er mogelijk een oplossing overblijft. In pseudo-programmeertaal (in de Perl source is dit de sub 'update_singles()'):

Zolang we nog/weer nieuwe cellen met een unieke waarde hebben doen we:
    Voor iedere cel met een unieke waarde doen we:
        Voor iedere groep waar deze cel in zit doen we:
            Wis de waarde uit de cellen in deze groep,
            behalve als het onze begincel met deze waarde is

Dit blijkt heel aardig te werken. Een simpele (3-sterren Sudoku) bleek met deze methode gelijk opgelost te worden.

En eenvoudig te programmeren, binnen twee uur typen/testen had ik dit geprogrammeerd en werkend (maar, ik had dus wel al voor die twee uur al een goed beeld van wat en hoe...).

Strategie 2

Helaas, voor moeilijker Sudoku's bleek dit niet afdoende te zijn. Wat weet ik nog meer voor strategieën?

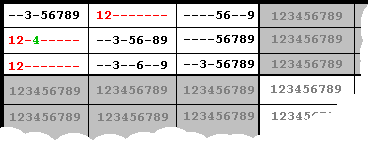Een aanvullende strategie is: als er binnen een groep een cel is met meerdere mogelijkheden, waarvan een mogelijkheid alleen maar in die cel van de groep voorkomt, dan moet die mogelijkheid ook de enige voor die cel zijn. Klinkt moeilijk, maar kijk het voorbeeld hiernaast: als er in een groep drie vakjes zijn met de mogelijkheden 421, 21, 21 (even aannemende dat in de andere vakjes van de groep ook geen 4 voorkomt), dan kan de 4 alleen nog maar in dat 421 vakje staan, en kan dat vakje dus geen 1 of 2 bevatten. Door dus de 4 alleen in deze cel te zetten (de 1 en de 2 te wissen) hebben we een nieuwe unieke waarde, en kunnen we strategie 1 weer toe gaan passen. Op een 5-ster Sudoku blijkt dit inderdaad het veld verder op te ruimen!

Weer het algoritme is pseudo-code (in het Perl programma is dit de sub 'check_uniques()'):

Zolang we nog nieuwe waarden vinden doen we:
    Voor alle groepen doen we:
        Voor alle cellen in die groep doen we:
            Als een symbool maar in een cel van de groep voorkomt,
            kunnen we de andere waarden in deze cel elimineren
    Als er iets gewijzigd is draaien we strategie 1 nog een keer

Ook weer relatief simpel, voor een mens. De werkelijke implementatie voor een computer is nog wel even denken, een simpel zinnetje als 'Als dit symbool maar in een cel van de groep voorkomt' is nog lastiger dan je zou verwachten. Wat ik doe is voor alle cellen in de groep, behalve de cel waarmee we bezig zijn) de patronen met een bitwise 'or' -functie combineren. Op die manier hebben we in een waarde alle symbolen die in die cellen voorkomen. Als we nu alle bits omdraaien hebben we de symbolen die juist niet in die cellen voorkomen. Door nu een bitwise 'and'-functie toe te passen met de cel die we aan het bekijken zijn, houden we die symbolen over die niet in andere cellen maar wel in deze cel voor komt. Met een beetje mazzel is dat er een, hebben we pech dan is dat er geen; zijn het er meer dan een dan klopt er echt iets niet...

Strategie 9999

Helaas, een 5-sterren Sudoku draait nog steeds niet... Dan weet ik nog maar een strategie: brute kracht... vandaar nummer 9999: als deze het niet vind, dan vind niets het (ultieme maar botte strategie). Hopelijk hebben de twee eerste strategieën al heel wat weggestreept (en we kunnen ze later nog vaker toepassen). Wat is de brute kracht methode? In principe heel simpel: voor iedere cel waar nog meerdere waardes mogelijk zijn gaan we ieder van die waardes gewoon proberen. Dus, weer een stukje pseudo-code (deze keer van de functie 'just_try()'):

Zolang we nog nieuwe waarden vinden doen we:
    Bewaar de huidige toestand van het bord;
    Voor iedere cel met meerdere waardes proberen we een voor een de mogelijke waardes
        Voor die waarde zetten de alleen die waarde in de cel,
        en passen we onze strategieën 1..3 op de zo gevormde toestand toe
        - Hebben we nu een oplossing dan zijn we klaar
        - Lukt het niet dan zetten we de bewaarde bord-toestand terug,
          en proberen de volgende waarde

Dit blijkt te werken!! Let op: we maken hier gebruik van 'recursie': deze functie kan zichzelf aanroepen (strategie 9999 gebruikt ook strategie 9999). Maar, omdat de cel waarmee we bezig waren op dat moment nog maar een waarde bevat (de waarde die we aan het proberen zijn), zijn er dus altijd minder mogelijkheden dan waarmee we begonnen, en zal de recursie altijd ophouden: of we vinden een oplossing, of we hebben geen mogelijkheden meer. En gezien we met deze methode automatisch alle mogelijkheden afgaan, moeten we bij een geldige Sudoku dus altijd het antwoord vinden.

En jawel, ook de 5-sterren Sudoku is nu in 2 seconden opgelost!

Een kleine update op 15 december 2006: het bleek dat bij sommige Sudoku's de strategie wat onhandig was geïmplementeerd; door de boven beschreven aanpak roept de routine zichzelf aan (recursie, strategie 3 gebruikt zichzelf); wat ook de bedoeling is, maar wat hier tot gevolg heeft dat er een zogeheten 'depth-first' zoektocht wordt gedaan. Dit geeft een (te) lange zoektijd. Daarom heb ik de recursie-diepte in het begin beperkt...

Invoer en uitvoer

Hoe krijgen we een Sudoku naar binnen? En het resultaat naar buiten? Een Sudoku is gelukkig niet zo veel typewerk, uiteindelijk zijn het maar 9x9 vakjes. Ik heb gekozen om de input via een bestand te doen, geeft ook de mogelijkheid eventuele extra regels toe te voegen (zie volgende hoofdstuk).  zie hier de input file van de boven besproken 3 sterren Sudoku:

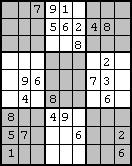
# 3-star sudoku for testing

@sudoku = (     # 9 regels
  "--791----",  # met 9 tekens
  "---56248-",
  "-----8---",
  "-------2-",
  "-96---73-",
  "-4-8---6-",
  "8--49----",
  "57---6--2",
  "1-------6",
        );

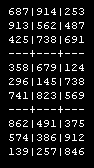
Afdrukken gaat in een soortgelijk formaat, zie hiernaast. Denk er aan; Perl is standaard een script-taal uitgevoerd via de DOS-prompt ofwel CMD window; ik heb er geen grafische user interface omheen gebreeën. Wat je hiernaast ziet is een screen capture van de output: de oplossing van de hierboven genoemde 3-sterren Sudoku.

Extra beperkingen -> nieuwe regels

Het is ook mogelijk nieuwe regels toe te voegen. Zo zijn er bijvoorbeeld Sudoku's met extra voorwaarden, bijvoorbeeld dat in extra gebieden de symbolen ook maar een keer mogen voorkomen. Dit kan op de diagonalen zijn, of in andere gebieden zoals de rode vakken in het figuur hiernaast. Dit kan mijn programma ook aan, door extra regels in de inputfile op te nemen (zie bijvoorbeeld de file ' sudoku_extra.txt' in onderstaande zip file).

Dit gebeurd door voor die gebieden de lijst met de nummers van de vakjes toe te voegen aan de bestaande lijst. De syntax hiervoor is vrij simpel: onderstaande regels komen uit sudoku_extra.txt:

# New constraints: 4 extra squares
push @rules, [ (10,11,12, 19,20,21, 28,29,30) ];
push @rules, [ (14,15,16, 23,24,25, 32,33,34) ];
push @rules, [ (46,47,48, 55,56,57, 64,65,66) ];
push @rules, [ (50,51,52, 59,60,61, 68,69,70) ];

Het programma sudoku.pl

Het programma (oorspronkelijke versie 1.4, voor een verbeterde versie zie verderop) is te downloaden als deze sudoku.zip, met daarin het Perl programma, en drie voorbeeld-Sudoku's (die hierboven genoemd zijn). Onbekend met Perl? Lees dan eerst mijn Perl pagina's.

Om het programma te draaien moet de Perl geïnstalleerd hebben. Dan, vanaf een command prompt (aannemende dat je de input in de file je_sudoku_input.txt hebt staan):

perl sudoku.pl je_sudoku_input.txt

Na wat tussenresultaten wordt vervolgens de oplossing afgedrukt (of een foutmelding als dit niet lukt; bijvoorbeeld door een type-fout in de input file).

Het programma zal de meeste types 3x3 Sudoku's aankunnen. Op dit moment kan het nog niet standaard andere vormen aan, zoals bijvoorbeeld dubbele Sudoku's met gedeeltelijke overlap. De strategieën zijn er OK voor, maar op dit moment is de 9x9 hier en daar nog hard er in geprogrammeerd (nummering van de vakjes moet uitgebreid worden). Technisch zeer wel mogelijk, maar voor mij op dit moment nog niet interessant.

Uitbreidingen

Grote Sudoku's (16 bij 16)

Soms zie je ook Sudoku's die groter zijn, met name 16x16 Sudoku's. Ondersteuning hiervoor is vrij eenvoudig toe te voegen, de regels zijn namelijk exact hetzelfde. In plaats van de grootte hard te coderen, is er nu een variabele $nrs geïntroduceerd, die standaard op 9 staat maar met de -l optie op 16 gezet kan worden. Ook de symbolen zijn in dat geval veranderd: in plaats van 123456789 gebruik ik 0123456789ABCDEF. Aanroep:

perl sudoku.pl -l grote_sudoku_input.txt

Een nieuwe strategie (nummer 3)

In maart 2009 heb ik een nieuwe strategie toegevoegd, met een functie genaamd check_pairs(). Bij het met de hand invullen van een Sudoku (ja, dat doe ik nog steeds) merkte ik dat ik deze strategie nogal eens gebruikte: Als je twee cijfers (symbolen) in nog maar twee vakjes van een regel hebt staan, dan weet je zeker dat een van die cijfers in het ene, en de andere in het andere hokje moet. Dus: er zijn naast deze twee geen andere cijfers in deze hokjes meer mogelijk, wat er verder nog staat kan worden weggestreept.

Best nog even lastig programmeren: je moet voor elke regel checken welke cijfers exact twee keer voorkomen, en dan voor ieder gevonden paar in die regel testen of ze beiden in twee dezelfde hokjes staan. Was even puzzelen (maar, daar gaat het dan ook om). Is uit te breiden naar andere versies (zelfde verhaal geldt bijvoorbeeld voor 3 cijfers en drie vakjes); heb ik echter nog niet gedaan.

En zowaar: de Sudoku's die ik tot nu alleen met brute force (strategie 9999) kon oplossen, worden nu opeens op deze manier gevonden (en een stukje sneller).

Verbetering in strategie 9999

Kleine verbetering: het programma checkt nu regelmatig of het bord nog geldig is (dus nergens 0 mogelijkheden heeft) met functie sanity_check(): is dit niet het geval dan hadden we verkeerd gegokt, en kan die poging (die recursie) afgebroken worden. Dit voorkomt dat er te lang wordt doorgerekend op iets waarvan we toch eigenlijk al kunnen weten dat het tot niets gaat leiden.

Meerdere oplossingen

Ook het zoeken van meerdere oplossingen is nu mogelijk, met behulp van de -a command line optie. Normaal kan dit niet voorkomen; mocht dit toch gebeuren dan is de Sudoku fout (of heb je een type-fout gemaakt bij invoeren). Bij een lastige 16x16 Sudoku (bedankt, Mies) bleek er inderdaad een fout te zitten in de oorspronkelijke puzzel: dankzij de nieuwe strategie 3 vond mijn programma twee geldige oplossingen (en dus klopte de Sudoku niet).

De verbeterde versie 1.6

Download hier Sudoku versie 1.6 programma en voorbeelden (maar, om Perl te leren misschien eerst de simpeler, oude versie proberen?)